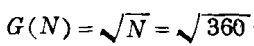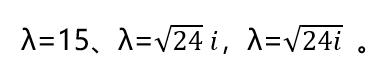洛书的数学研究之三 ——焦氏《河洛数论》探源（续）

发布时间：92年09月25日

焦蔚芳编译陈花芬朱明基

三、洛书数论要义

1. 洛书数的集合论

A. 洛书数的置换（Permutation）

在数学中，数1，2，3…，n的置换的研究为所有各类变换的研究提供了一个基础。我们用：

表示置换σ。由于σ是一一对应且及其本体的，因而序列i₁，i₂……i_n是数1，2……，n的一个排列。n阶置换的排列数为n！。例如了阶置换是：（123），（132），（213）（231），（312），（321）。即3！=1 · 2 · 3=6。

置换σ的特征包括其反序数、奇偶性符号及其循环因子等。置换σ的一个反序是整数1 · 2，…，n中的一个序偶（p，q），虽然p＞q，但在σ中p却位于q前。我们用I（i₁，i₂……，i_n）表示σ的反序数，而σ的符号或其奇偶性则用关系式sgnσ=（-1）I^{（i1，i2……，in）}的正负来决定。 - 1为奇数I，+1为偶数I。置换又可表示为没有公共元素的一些不相交循环的乘积形式，称为循环因子分解。例如置换

可分解为（1，4，3，6）与（2，5）。

现在让我们将置换操作应用于洛书数集L₉={1，2，3，4，5，6，7，8，9}，并用S₉表示L₉的所有置换的集合。S₉的排列数=1 · 2 · 3…9=362880. 根据洛书矩阵论^{[ ]}、群S₉可分为四个子群：ⅰ）洛书本体 · ⅱ）洛书变体 · ⅲ）自然洛书 · ⅳ）杂体洛书。S₉的特微性质说明如下：

（a）从自然洛书到洛书本体的置换：在群S₉中，

同样A^-1A=E。

让我们用L_p=<4，9，2，3，5，7，8，1，6>表示洛书本体的置换，它的反序数I（4，9，2，3，5，7，8，1，6）=17，因而它的符号是-1。在置换A中我们看出将1→4，4→3，3→2，2→9，9→6，6→7，7→8，8→1且5→5。因此洛书本体的置换可表示为两个循环因子（1，4，3，2，9，6，7，8）与（5）之积。

（b）S₉的特微性质：原文列出了S₉的四个子群的某些置换的特微性质，包括各置换的反序数、符号与循环因子等，其中有些关系是令人感兴趣的，因篇幅关系，此处从略。

（c）S₉的置换的乘法：置换的乘法是由一给定的置换形成新置换的程序，如我们将某置换A施加于S₉的任一元素x，然后再将置换B施加于新元素xA得（xA）B。如果将x直接置换成（xA）B的置换称为A与B的乘积AB，根据定义我们有x（AB）=（xA）B。置换的乘法与数的乘法有某些类似，但必须注意，在数的乘法中交换律与结合律都是真的，而置换乘法则服从于结合律而不服从交换律，因为置换乘法与因子顺序有关，x（AB）≠ x（BA）。

B. 洛书数的整除（Aliquot）性：

为了研究数的整除性，我们要知道一个数的约数以及一个数集的最大公约数（g，c，d，）与最小公倍数（i，c，m，）。用符号d=（a，b）表示a，b两数的g，c，d.；符号m=[a，b]表示a，b两数的l，c，m.，d与m之间的关系可以用公式d · m=（a，b）[a，b]=a · b来表示。

（a）洛书数集的g，c，d，与l，c，m. ：将上述的定义与运算公式应用于洛书数集L={1，2，3，4，5，6，7，8，9}，我们写出这些数的素因子分解式L={1，2，3，2²，5，2 · 3，7，2³，3²}。L的g，c，d仅可能是d=（1，2³，3²，5，7）的极小值，因而d=min（L）=1，亦即洛书数集L中除1之外无其他公因子。L的l，c，m，可以用m[L]=max [L]=[2³，3²，5，7]=2520来表示，从几何上说，若我们取360作为绕一圆旋转一周的值，则洛书的l，c，m，=7.360，即包含七周之值。

（b）洛书数的9，c，d，与l，c，m，的集合论：在运算d=（a，b）与m=[a，b]中，当数a与b分别按照分解式a=π_iP_i^ai与b=π_iP_i^Si时，它们的g，c，d，与l，c，m，将分别由d=π_iP_i^min^{（αi，βi）}与m=π_iP_i^max^{（αi，βi）}来计算，因而d与m的运算可归结为形成α与β的最小与最大值。再进一步，引入集合运算中的算子∪（并）与∩（交），从而建立关系d=（a，b）=a∩b；m[a，b]=a∪b。如此则d与m的运算又归结为集合运算。

我们概括三种类似的运算系统得ⅰ）d=（a，b）；m=[a，b]。ⅱ）d=min（α，β）；m=max[α，β]。ⅲ）d=a∩b，m=a∪b。所有这些运算将满足集合论的某些简单规律如幂等律、交换律、结合律与吸收律等。

（c）数“360”的整除性：在洛书数论中，我们常将360作为一个泛常数，这是根据两大理由：ⅰ）洛书矩阵的行列式值是360。ⅱ）洛书数集的l，c，m，是7×360。所以360的约数同洛书数的多种算术运算是相关的。令N=360，得到N的约数的一些关系式例如：N的约数的几何平均值

N的约数的算术平均值A（N）=1170/24；N的约数的调和平均值H（N）=360×24/1170=96/13，以及关系式N=A（N）· H（N）；A（N）≥G（N）≥H（N）等等。

2. 洛书数的矩阵论

A. 洛书作为线性变换的过渡矩阵（Transition Matrix）

设V与W是域k上的矢量空间，则变换T：V→W是从矢量空间V到另一矢量空间W的一个映射，而函数F如满足条件：ⅰ）F（v₁+v₂）2 F（v₁）+F（v₂）；ⅱ）F（av₁）=a F（v₁）。（v₁，v₂∈V；a∈K），则F：V→W为一线性变换。根据上述的原则、我们阐明洛书矩阵作为一个线性操作的要义如下。

（a）洛书矩阵表示一个线性变换。根据定义：每个线性变换T：V→W都有一个与之相关联的代表矩阵，亦即每个线性变换都可用一个矩阵来表示。而该代表矩阵则取决于接受T操作的V空间的基底矢量，亦即每个矩阵也表示关联于某一基底的线性变换。

我们引入矢量空间其基底变换的定理：设P是从矢量空间V内的一个基底｛e_i_｝到另一个基底｛f_i_｝的过渡矩阵，则对任意矢量v∈V，我们有P[v]_f=[v]_e_。如以洛书矩阵作为P，洛书矩阵作为空间V内从卡氏基底｛e₁，e₂，e₃_｝到洛书基底｛f₁，f₂，f₃_｝的过渡矩阵，可以证明上述定理。另外，根据上述关于线性函数F的条件可证明洛书函数F（x，y ，z）=（4x+9y+2z， 3x+5y+7z，8x+y+6z）为一线性函数。于是得出结论：洛书矩阵表示了相关于三维洛书基底的一个线性变换。

（b）线性映射（Linear Mapping）的核（Kernel）与将像（Image）：定义：ⅰ）设F：V→W是一个线性映射，F的像是由V映射到W的像点群，记作ImF={w∈W：F（v）=w，v∈V}。ⅱ）F的核是映射到0∈W的V中的元素群，记作Ker F={v∈V：F（v）=0}。定理：设F：V→W是一个线性映射，则F的像是W的一个子空间，它的核是V的一个子空间，且dimV=dim（Ker F）+dim（ImF）。式中dim表示维数。

我们通过由T：R³→R³与T（x，y，z）=（4x+9y+2z，3x+5y+7z，8x+y+6z）定义的洛书映射验证上述定理。（计算从略）

（c）可逆算子（Invertible Operator）；一个线性算子T：V→V称为可逆的，如果它有一个逆算子，亦即存在T^-1∈A（V）将，即得TT^-1=T^-1T=I（I是V上的恒等算子）。

一个线性映射如果它的核是零矩阵亦即dim（Ker F）= 0时，我们称它是非奇异的。以映射的奇异性为基础我们得到两个定理：ⅰ）一个线性映射，当且仅当它是非奇异的特是一个同构（Isomorphism）（即一一对应）。ⅱ）一个有限维矢量空间上的线性算子，当且仅当它是非奇异的时，T：V→V是可逆的。

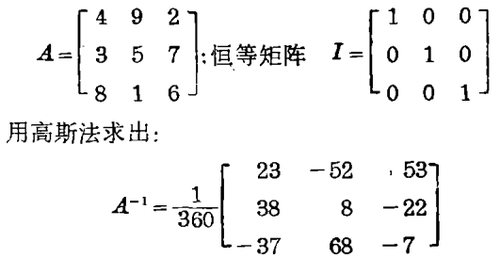
应用上述原则我们可以找到洛书变换T（x，y ，z）的逆变换。同T相关的矩阵是：

即文献［6］中的洛书逆矩阵Q。

根据洛书矩阵是非奇异的、进而证明A是一一的，因而洛书线性变换T（x，y，z）应是一个同构。

（d）相似性变换。洛书表示向量空间V内从基底｛e_i_｝到基底｛f_i_｝的过渡矩阵P，由于P是可逆的，从而对V上的任意线性算子T我们有[T]_f=P^-1[T]_eP，相应要，若A是V上的一个线性算子T的任一矩阵表示，则矩阵B=P^-1AP也是T的一个矩阵表示，从而B称为相似于A，或称为由A通过相似性变换而得B。

矩阵的相似性是一个等价关系，即线性算子T的所有矩阵表示形成一个相似矩阵等价类。这个原则应用于洛书矩阵，我们推得：洛书矩阵的所有72种形式组成一个相似矩阵的等价类。

B. 线性映射与线性方程组。

线性映射的重要应用是解线性方程组，域K上的一个含n个未知数、m个线性方程的方程组可以写成矩阵方程AX=B，它伴随的齐次方程组用AX=0表示。系数矩阵A可看作为B∈K在线性映射A：Kⁿ→K^m下的原像（preimage）；而齐次方程组AX=0的解可看作为线性映射A：Kⁿ→K^m的核。

如m=n=3，即A为-3阶矩阵——洛书矩阵。应用上述定则，可以得出：在三维空间K³内，洛书矩阵提供了在用线性映射求解线性方程组时的一切可能场合。

C. 洛书矩阵的不变量。

在研究矩阵与线性变换时，曾发现某些代数式的集合，它们在通过一个线性变换时是不变的。这些函数一般被称为特征函数，它们是由在线性变换下不变的性质所构成。因此当吾人寻求可表达线性变换内在性质的数学式时，可用求取代数不变量来代替上述问题。由于洛书数的奇幻性质，洛书矩阵内就蕴涵着一些不变量。现列举洛书矩阵的不变量的三种类型如下。

（a）几何不变量：洛书的几何不变量包括其基矢矢长，基矢数性积、矢性积以及基矢间的夹角等，详见洛书几何学。

（b）洛书矩阵的行列式值：洛书本体的行列式值为360，而自然洛书的行列式值为0，其流转关系详见洛书矩阵论。

（c）洛书矩阵的特征方程与特征值：设T：V→V是域K上的矢量空间V内的一个线性操作；且设它在—个已知基底上的代表矩阵为一个n阶方阵A。如果存在一个非零矢量v∈V使A（v）=λv，则纯量λ∈K称为A的一个特征值。使λ成为A的特征值的必要与充分条件是：算子λI_n-A为非奇异的。（其中I_n是n阶的单元方程）矩阵[λI_n-A]称为A的特征矩阵，它的行列式值｜λI_n-A｜是λ的一个多项式。（λI_n-A）=0称为A的特征方程、它的根就是特征值。

由上述定义（λI-A）=0求出洛书矩阵的特征方程为λ³-15λ²+24λ-360=0。A的特征值为

其中取实数λ=15，该数正是洛书中各三序组数字之和，也是从坐标原点到洛书三角形各项点的距离。

结论

世界古代数学史指出，古代中国人曾致力于数型的研究并创造了两个数图：河图与洛书。这两个图阵展示了几千年前古代中国人在数理抽象方面的非凡业绩。但不幸的是，自从这两个图阵出现以后，却没有一篇文章用现代数学观点来解释它们。有鉴于此，作者认为：通过现代数论对这两个图进行数学研究是十分必要的也是很有意义的。基于研究结果，作者导出本文“《河、洛数论》探源”。

关于河图研究的结论是：

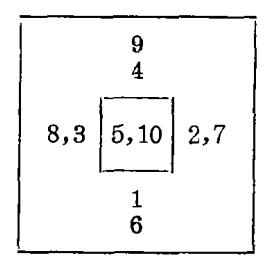
（1）河图表示十个数的集合：H={1，2，3，4，5，6，7，8，9，10}，以及由R_h={（1，6），（2，7），（3，8），（4，9），（5，10）}={（x，y）；y=x+5；x，y∈H｝所表示的它的元素间的泛函关系。

（2）河图中的十个数由五个序偶合成并排列成由一水平行与一垂直列组成的十字形，它可以揭示数的X-Y坐标的原始概念。

（3）河图表示以e₁=（l，2）与e₂=（3，4）作为最小基底的一个二维矢量空间。

（4）河图表示以模5同余的商集Z/R₅。

（5）河图提供了整数直角三角形的毕氏定理的基础。

关于洛书的研究结论是：

（1）洛书图阵是由1到9的九个数字组成的具有幻方特性的3×3阶矩阵。

（2）洛书表示九个数的集合L={1，2，3，4，5，6，7，8，9}，它的各元素间的基本泛函关系为R_l={（x，y，z）；x+y+z=15；x，y，z∈L}。

（3）洛书是由它的三个列矢量（4，3，8）；（9，5，1）；（2，7，6）或三个行矢量（4，9，2）；（3，5，7）；（8，1，6）张成的三维矢量空间的代表矩阵。

（4）洛书表示数的十进制。

（5）洛书表示以模10同余的商集Z/R10。